

The table also indicates that the final y-velocity (v fy) has the same magnitude and the opposite direction as the initial y-velocity (v iy). This is due to the fact that the horizontal velocity of a projectile is constant there is no horizontal acceleration. In this case, the following information is either explicitly given or implied in the problem statement:Īs indicated in the table, the final x-velocity (v fx) is the same as the initial x-velocity (v ix). The solution continues by declaring the values of the known information in terms of the symbols of the kinematic equations - x, y, v ix, v iy, a x, a y, and t. In this case, it happens that the v ix and the v iy values are the same as will always be the case when the angle is 45-degrees. The solution of any non-horizontally launched projectile problem (in which v i and Theta are given) should begin by first resolving the initial velocity into horizontal and vertical components using the trigonometric functions discussed above. Determine the time of flight, the horizontal displacement, and the peak height of the football. To illustrate the usefulness of the above equations in making predictions about the motion of a projectile, consider their use in the solution of the following problem.Ī football is kicked with an initial velocity of 25 m/s at an angle of 45-degrees with the horizontal. The topic of components of the velocity vector was discussed earlier in Lesson 2. sine(Theta) where Theta is the angle that the velocity vector makes with the horizontal.The initial y-velocity (v iy) can be found using the equation v iy = v i cosine(Theta) where Theta is the angle that the velocity vector makes with the horizontal.The initial x-velocity (v ix) can be found using the equation v ix = v i In each of the above equations, the vertical acceleration of a projectile is known to be -9.8 m/s/s (the acceleration of gravity).Īs discussed earlier in Lesson 2, the v ix and v iy values in each of the above sets of kinematic equations can be determined by the use of trigonometric functions. An application of projectile concepts to each of these equations would also lead one to conclude that any term with a x in it would cancel out of the equation since a x = 0 m/s/s.įor the vertical components of motion, the three equations are The other two equations are seldom (if ever) used. Of these three equations, the top equation is the most commonly used. For the horizontal components of motion, the equations are You may recall from earlier that there are two sets of kinematic equations - a set of equations for the horizontal components of motion and a similar set for the vertical components of motion. To treat such problems, the same principles that were discussed earlier in Lesson 2 will have to be combined with the kinematic equations for projectile motion. A non-horizontally launched projectile is a projectile that begins its motion with an initial velocity that is both horizontal and vertical. In this section of Lesson 2, the use of kinematic equations to solve non-horizontally launched projectiles will be demonstrated. These equations were used to solve problems involving the launching of projectiles in a horizontal direction from an elevated position. Their conception of motion encourages them to think that if an object is moving upward, then there must be an upward force and if an object is moving upward and rightward, there must be both an upward and rightward force.In the previous part of Lesson 2, the use of kinematic equations to solve projectile problems was introduced and demonstrated. Note: Students should avoid confusion with the concept that the only force acting upon an upward moving projectile is gravity. The method to analyse two-dimensional projectile motion is to break it into two motions: one along the horizontal axis and the other along the vertical axis. The most important fact to remember here is that motions along perpendicular axes are independent and thus we can analyse them separately.
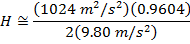
We consider two-dimensional projectile motion, and we neglect the effects of air resistance. Such objects are called projectiles and their path is called a trajectory. There are many uses of projectile motion in mechanics. Projectile motion is the motion of an object thrown or projected into the air, only under the gravitational acceleration. Now the velocity vector after time t is given by,


 0 kommentar(er)
0 kommentar(er)
